Function Composition And Inverse Functions¶
Function composition and inherited domain and range¶
Source: I made this problem up
Explanation:
This artifact demonstrates function composition and inherited domain and range.
I present two different funtions, and I give their individual domain and range.
Then, I compose them (\((f \circ g)(x)\)), and show the inherited domain and range of the new function.
The domain of \((f \circ g)(x)\) is usually the domain of \(f(x)\) and the range of \(g(x)\),
but in this case, it is only the positive portion because \((f \circ g)(x)\) has a radical, and the domain of any radical is \(x \geq 0\)
Independent Thinking:
This artifact also demonstrates independent thinking because its’ source code uses quite a few LaTeX expressions that I didn’t know how to use at the time.
I went through the source code of another LaTeX document I found online and figured out how to use latex expressions in my code.
Artifact:
Find \((f \circ g)(x)\)
Function decomposition¶
Source: I made this problem up.
Explanation:
In this artifact I demonstrate how a function can be decomposed into two different functions.
It’s not easy for me to show my work on this problem, but basically what I did is compose two new function that would evaluate to \((f \circ g)(x) = \sqrt{x^2 + 3}\).
I can still check my work by plugging in g(x) into f(x):
\(f(g(x)) = \sqrt{x^2 + 3}\)
Awareness and appreciation:
There is potentially an infinite amount of solutions to this problem, but this is probably the best solution for two reasons.
- It is the simplest solution
- Because it is the simplest solution, it is also the easiest to re-compose into the original function.
Artifact:
Decompose \((f \circ g)(x)\)
Parametric functions and how they relate to function composition¶
Source: Question #4 from 1.5
Explanation:
The first example demonstrates: How to find an (x, y) pair when given a parametric function and a t value.
The second example demonstrates: How a linear function can be composed from a parametric function by eliminating the parameter.
All I have to do is solve for t and plug t back into one of the original equations.
Artifact:
Find the (x,y) pair for the value of the parameter
\(x = t + 3\) and \(y = {1 \over t}\) for \(t = -8\):
Eliminate the parameter:
Inverse functions and inherited domain and range¶
Source: Section 1.5: Example 4
Explanation:
This artifact demonstrates inverse functions and inherited domain and range.
I present a regular function, and I show its’ domain and range.
Then I invert it, and show that the domain and range of the result is the inverse of the original function.
Appropriate Use of Technology
I used an online graphing calculator to generate the graph below.
Once I generated it:
- I took a screenshot of the online graph
- I cropped the screenshot
- I added the image to my local code repository
- I included the image in my source code
- I uploaded the image to my code repository (https://github.com/doubledubba/precalc) and updated my code
- I synchronized my readthedocs.org project with my repo
Numeric Algebraic Graphic Connection (N.A.G.)
I used a graph to show the N.A.G. connection between the original function and the inverse function.
The red one is the original function, and the yellow one is the inverse function.
Artifact:
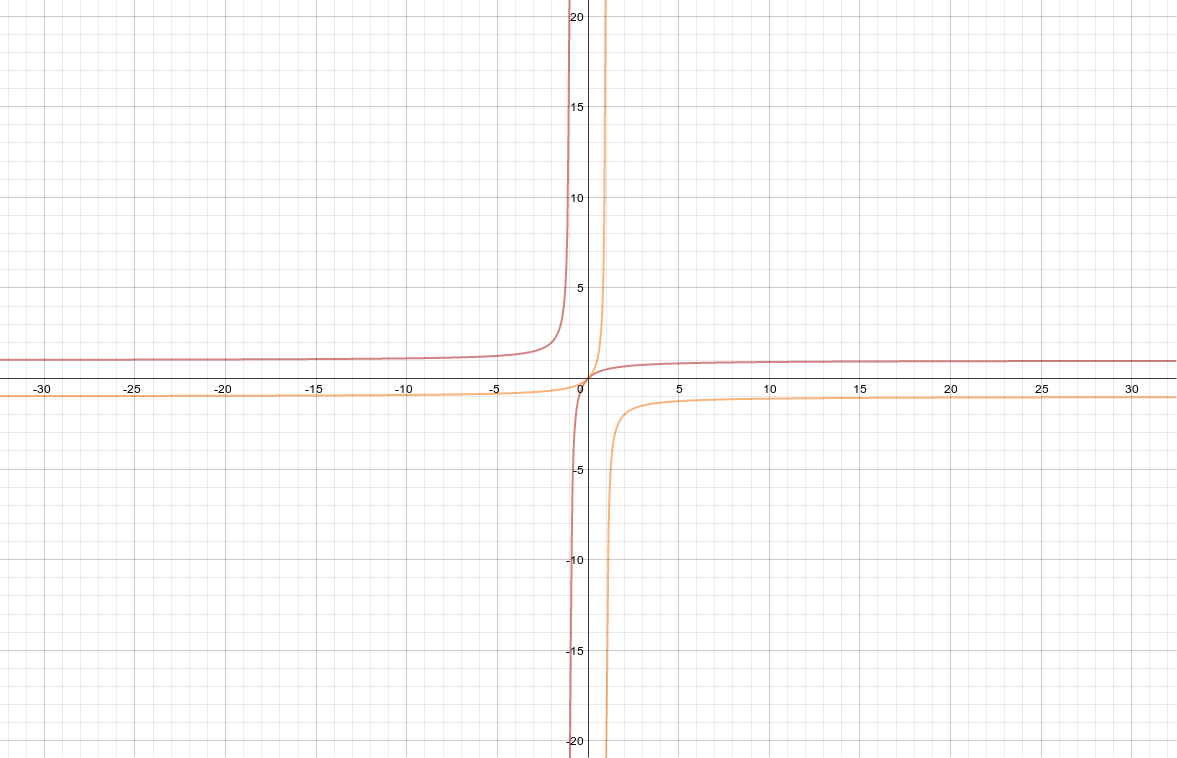
Find an equation for \(f^-1 (x)\) if \(f(x) = {x \over (x+1)}\).
Domain: \((-\infty, -1), (-1, \infty)\)
Range: \((-\infty, 1), (1, \infty)\)