Power Functions, Their Graphs And Applications

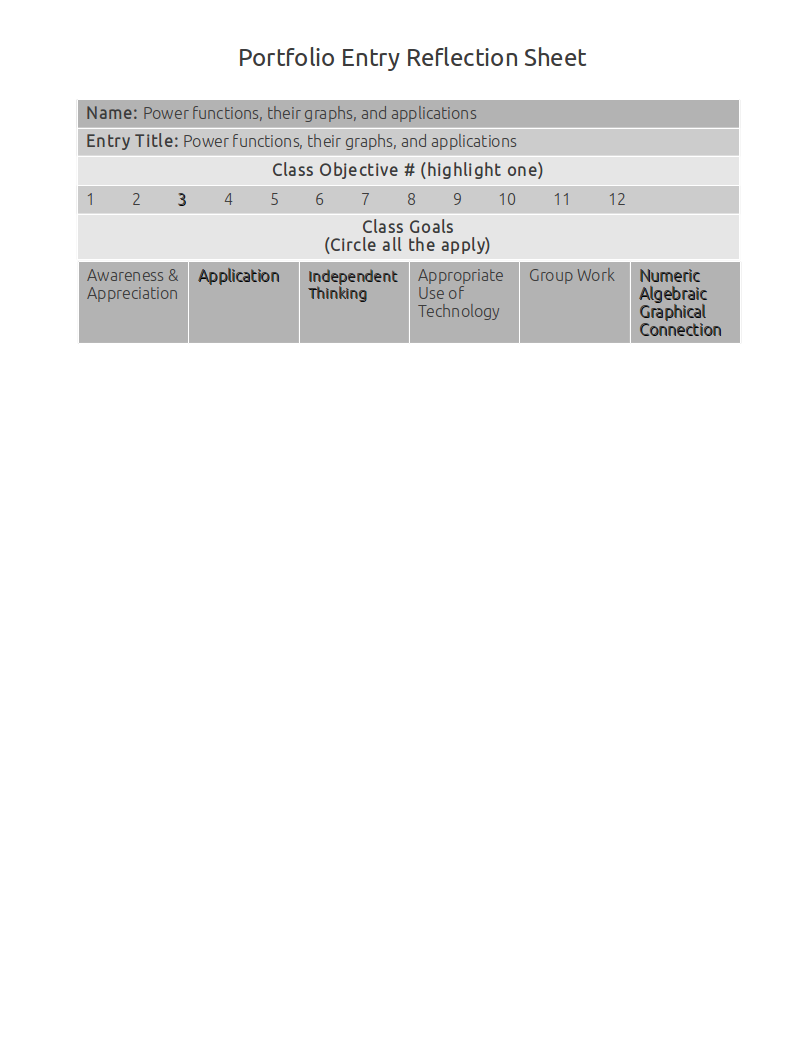
Graphs of different power functions

Source: Section 2.2 Figure 2.14

Explanation:

This artifact demonstrates graphs of different power functions (\(y = a*x^n\)).

There are really four different ways that power functions will look like.

The orange function is one where \(n < 0\).

The red on is where \(n > 0\)

The green one is where \(n = 1\)

The purple on is where \(0 < n < 1\)

Artifact:

Orange: \(y = x^-1\)

Red: \(y = x^2\)

Green: \(y = x^1\)

Purple: \(y = x^{1 \over 2}\)

Writing a power function from a list of data

Source: Chapter 2 Test Non Calculator #1, and python code

Explanation:

This artifact demonstrates writing a power function from a list of data.

I got the first statement (\(2^n = {1 \over 4}\)) from the first two points in the data set.

In the x, \(1x = 2\\x = {2 \over 1} = 2\)

In the y, \(32x = 8\\x = {8 \over 32} = {1 \over 4}\)

From there I infer that \(2^n = {1 \over 4}\), solve for n, and compose a power function.

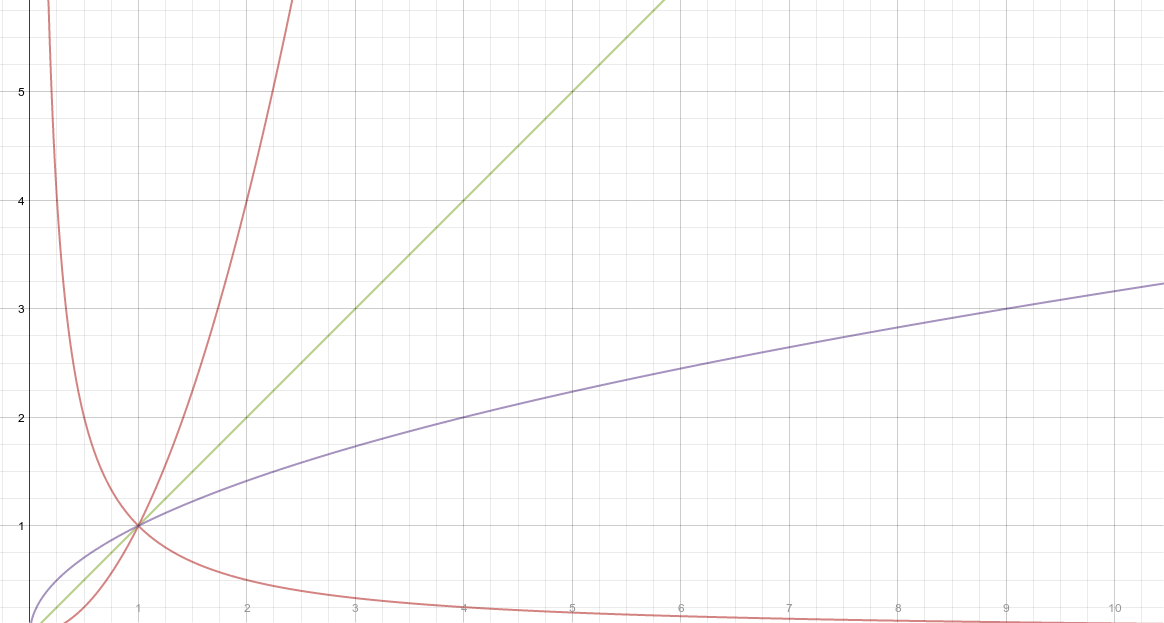
Numeric Algebraic Graphic Connection

My function is backed up by this graph (look at 2,8 - it matches the data set):

Application and Independent Thinking

I wrote a python script to validate my function.

This demonstrates Application because I was able to apply this math problem into a program, which is a very usefull skill.

It also demonstrates independent thinking because I taught myself how to write python code.

It runs successfully:

points = (  # dataset
    (1.0, 32.0),
    (2.0, 8.0),
    (6.0, 8.0/9.0),
    (8.0, 0.5),
    (10.0, 0.32),
)

def f(x):  # This is a function. A x value gets plugged in, and a y value comes out.
    return 32.0*x**-2  # same as 32*x^-2

for x,y in points:  # This is a recursive loop. x and y are variables points from our dataset
    assert y == f(x)  # If y is not equal to f(x), then the program will fail.

Artifact:

x	y
1	32
2	8
6	8/9
8	0.5
20	0.32

\(2^n = {1 \over 4}\\ n = -2\\ 8 = a2^{-2}\\ a = 32\\ y = 32x^{-2}\)

Applications of power functions through direct or indirect variation

Source: Chapter 2 Test (calculator portion) #2

Explanation:

This artifact demonstrates applications of power functions through direct or indirect variation.

From reading the problem, I could infer that (0.6, 14) was a point on the graph of the power function being described.

I understand as well that the function would be a function of length squared, and that is how I got the algebraic function.

Using my first observation of the point on the line, I plugged in what I knew about the previously defined algebraic function (x and y).

At that point, I was able to solve for the only remaining variable, the constant of variation.

Having been provided the power of the x in the problem, and having solved for the constant of variation, I was able to compose the formula \(s(l) = 39.89 * l^2\)

From there, it was only a matter of solving for s(0.65) to answer the question.

Application

This problem demonstrates the application of a classroom math problem to a real life situation.

Artifact:

The top speed at which a person can sprint varies directly as the square of their stride length.

If a person can run at a top speed of 14 mph with a stride length of 0.6m,

how fast can she run if she increases her stride length to 0.65 meters?

\(s(l) = a*l^2\\ 14 = a*0.6^2\\ a = 38.89\\ s(l) = 39.89l^2\\ s(0.6) = 13.969 \text{ mph}\\ s(0.65) = 16.393 \text{ mph}\)